Jasper Johns (Augusta, Georgia, USA, 1930 - ) - Numbers

Numeri utili e numeri inutili (4)

di Silvio Hénin

Comincerò con un brevissimo raccontino. L’idea non è mia, ma di un caro amico lontano, che mi ha concesso i diritti di riproduzione.

“Il signor Rossi sentì un rumore proveniente dalla cucina. Andò a vedere. Dal rubinetto del lavello usciva un torrentello d’acqua. Provò a stringere la valvola, ma niente da fare, la cascatella non accennava a diminuire. Provò allora a chiamare un idraulico, ma era la Vigilia di Natale e non ne trovò nessuno, salvo quelli di pronto intervento. “Troppo cari” pensò e decise allora di rinviare la riparazione “Tanto l’acqua va giù dallo scarico”. Andò a dormire, pregustandosi il cenone della sera dopo, ma a metà notte fu risvegliato dallo sciacquio e decise di controllare la situazione. Era decisamente peggiorata, adesso anche lo scarico sembrava non smaltire più la perdita e il livello nella vaschetta continuava ad aumentare. “Qui ci vuole un intervento drastico”, si disse  e andò in cantina a chiudere la valvola principale. La perdita sparì. “Problema risolto!”.

Il mattino successivo Rossi realizzò che però non poteva lavarsi e neppure prepararsi un caffè. Questo non era tollerabile neppure per un giorno, era un limite alle sua libertà costituzionali. Il problema era stato risolto, no? Adesso la perdita si era fermata! Quindi andò in cantina e riaprì la valvola generale. La perdita ricominciò, ma sembrava compensata dallo scarico. Si lavò, bevve il caffè e uscì per fare un giretto. Quando tornò e aprì la porta di casa, si accorse subito che un leggero strato d’acqua copriva tutto il pavimento e il lavello, ormai pieno, traboccava in una cascatella continua. “Forse non dovevo riaprire” si disse e, preso dal panico andò ancora in cantina per richiudere la valvola centrale, ma senza riuscirci, si era bloccata anche quella.

Finalmente, arrivò l’idraulico, uno di quelli disponibili 24 ore per 365 giorni all’anno (366 nei bisestili), trovato su Internet.  L’artigiano lavorò per mezz’ora, per un totale di 500 euro, compresi i pezzi di ricambio. Le spese però non finirono qui, Rossi dovette anche rifare il pavimento della sua cucina, le cui piastrelle si erano sollevate, e dovette rimborsare il condomino sottostante per i danni al soffitto. Ben più di 500 €!”

Penso che sia chiaro a tutti il significato della metafora.

Eccoci in prossimità delle festività natalizie e al loro corredo di assembramenti. Ci si affollerà per lo shopping, nei negozi e nei mezzi di trasporto, ci si riunirà per i festeggiamenti di Natale e, ancor più per quelli di San Silvestro, con una coda alla Befana.  Bene ha fatto il Governo a imporre una continuazione del lockdown, ma a mio parere (e non solo mio) il nuovo DCPM è arrivato troppo tardi e le sue regole sono ancora troppo lasche, timide, confuse e impossibili da controllare.

La giustissima preoccupazione per l’economia  e le grida di allarme che si levano da gruppi di imprenditori, artigiani e dei loro dipendenti e fornitori costringe il potere politico a mediare. La politica, si sa, è l’arte del compromesso. Purtroppo, sembra che non si capisca che una terza ondata, ancor più violenta della prima e della seconda, avrebbe effetti economici ancor più drammatici e per più lungo tempo. Per dirne solo un paio, la produzione e la distribuzione si potrebbero trovare con meno clienti, con meno dipendenti e meno fornitori; i costi per la sanità esploderebbero, lasciando un debito pubblico enorme che tutti dovremo pagare con le tasse nel prossimo decennio (almeno per chi le paga).

Torniamo però a parlare di numeri, visto che è su questi e sulla loro interpretazione che si basano sia le decisioni del governo sia le obiezioni delle opposizioni. Un primo problema relativo alla interpretazione nasce spesso dalla modo di presentare i dati. Per un esempio di come l’esposizione possa indurre a una interpretazione sbagliata vi mostro tre grafici e vi propongo un quiz.

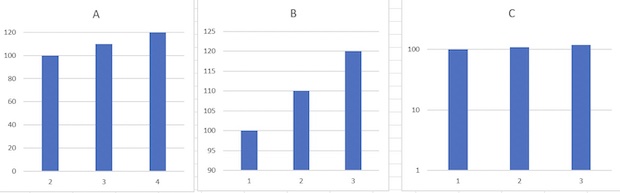
Quiz: a prima vista, quale grafico rappresenta la crescita più veloce e quale la più lenta? (La risposta esatta la troverete alla fine del testo).

Ogni giorno vediamo pubblicati molti dati in forma tabellare o in forma di grafici, ma alcuni (magari proprio quelli che vengono ripresi nei titoli), hanno un significato ben scarso e possono essere interpretati in modi differenti. Prendiamo un esempio: la percentuale di nuovi casi rispetto al totale dei casi già contati, la tipica affermazione è “Oggi ci sono stati 24.756 nuovi casi, pari a un incremento del 17,5% (ieri era del 21,4%)”, la conclusione che viene spontanea è: “La situazione sta migliorando”. Ma non è così. Per prima cosa, e non mi stancherò mai di ripeterlo, il numero 24.756 ci dice solo quanti nuovi casi si sono ‘scoperti’, non quanti sono in realtà. Ma anche se avessimo fatto il tampone a tutti gli italiani, la conclusione sarebbe sbagliata. Vediamo perché.

Immaginiamo di partire da 1000 casi (reali) e che ogni settimana se ne aggiungano 100. Alla fine della prima settimana l’incremento sarà del 10% (1100/1000), la seconda settimana sarà del 9% (1200/1100) e la terza del 8,3% (1300/1200). Le tre percentuali, se paragonate, danno la falsa impressione che la situazione stia migliorando, ma il calo della percentuale significa in realtà un aumento lineare del numero di casi e dopo 10 settimane il numero totale dei casi sarà raddoppiato. Ecco la tabellina:

Se invece la percentuale di aumento resta costante è ancora peggio, significa che la crescita è addirittura esponenziale, indice del disastro che abbiamo vissuto in ottobre e novembre, almeno in alcune regioni! Vediamolo in un’altra tabellina.

E il numero di contagi  raddoppierebbe in sole sette settimane.

Come già detto, anche il numero di casi postivi di ogni giorno vuol dire ben poco, infatti vi sono compresi anche tutti i tamponi ripetuti più volte sugli stessi individui. Si pensi al solo personale sanitario, che ripete il tampone più volte al mese (con grande variabilità da regione a regione). A questi si aggiungono tutti i malati già noti, ricoverati o in quarantena. Giustamente, il numero di nuovi casi giornalieri è depurato dalle ripetizioni del test su casi già noti, ma non è così per il numero di tamponi, ne deriva che il loro rapporto è fuorviante.

Ad esempio: il giorno 2 dicembre, in Lombardia sono stati eseguiti 36.077 tamponi totali, ma solo 10.769 di questi non erano ripetizioni. Se ci riferiamo al primo numero, il rapporto positivi/tamponi totali era 9,5% (uno su dieci circa), ma se confrontiamo con il secondo il rapporto positivi/nuovi casi testati diventa 31,8%, tre volte maggiore del primo e dieci volte più di quel 3% che si dovrebbe raggiungere per decretare la fine della seconda ondata.  Dai pochi dati incompleti che si conoscono si può dire che i tamponi fatti su ‘nuovi’ casi oscillano da un terzo alla metà del totale giornaliero, ma il numero varia molto a seconda del giorno e della regione.

Preferisco misurare il tempo in settimane, non in giorni, per due importanti motivi. Il primo è che, come credo di aver già detto, le oscillazioni tra un giorno e l’altro sono sempre ampie e casuali. Come sapete, la raccolta dei dati è affidata alle singole regioni, mentre l’elaborazione dei totali viene fatta centralmente. Questa schizofrenia è causa di rilevanti imprecisioni dovute ai diversi tempi e metodi usati dalle amministrazioni regionali, che raramente agiscono in sincronia. Quindi, quelli che vengono definiti dati ‘di ieri’ possono essere tali solo in alcune regioni ed essere di due giorni prima o più in altre. Prendendo le medie settimanali questa anomalia tende a sparire.

Esiste una seconda causa di variabilità, questa volta non risolvibile: la discronia che esiste tra gli eventi esaminati, cioè i ritardi tra il momento dell’infezione, quello della positività del tampone, l’insorgenza eventuale di sintomi, la fase di infettività (trasmissibilità ad altri), l’aggravamento che porta alla terapia intensiva e il decesso. Il divario si misura in settimane (da tre a quattro almeno), per cui un decesso di oggi può riferirsi a un tampone positivo di un mese fa e a una ospedalizzazione di 20 giorni fa. In generale, questo significa che l’effetto di qualunque misura adottata per il contenimento dell’infezione potrà essere osservato solo dopo un mese.

È una sorta di ‘inerzia’ statistica che rende anche molto difficile fare previsioni attendibili basate su modelli matematici. Leggevo ieri su un quotidiano che un ‘esperto’ prevedeva la fine della seconda ondata entro la metà di gennaio 2021, “se saremo bravi”, ma è pura fantasia. Molto più credibile la previsione di altri suoi colleghi che paventano una terza ondata tra gennaio e febbraio. Quanto alla differenza tra ‘prima’, ‘seconda’ e ‘terza’ ondata, ricordo che per alcuni storici la Seconda guerra mondiale fu solo una inevitabile continuazione della Grande guerra del ‘15-‘18. Credo che lo stesso valga per le ondate della pandemia, in entrambi i casi le cause di base non erano sparite.  

Veniamo ai vaccini. Anche qui cominciano a fioccare i numeri: percentuali di efficacia, numero di dosi, tempi di consegna e tempi di somministrazione. E si fa una grande confusione. L’efficacia è valutata dalla sperimentazione di Fase 3, eseguita su decine di migliaia di volontari, moltissimi ma non statisticamente rappresentativi dei 7,5 miliardi di esseri umani che vivono oggi sulla Terra. Intere categorie di persone non vi sono rappresentate. Quanto alla somministrazione, per raggiungere in Italia l’immunità di gregge (che brutta parola) si dovrebbe vaccinare almeno il 90% della popolazione, cioè somministrare almeno 100 milioni di dosi (50 milioni per due volte). I vaccini devono però essere ancora approvati dalla EMEA, devono essere prodotti, devono superare i controlli di qualità, devono essere distribuiti sul territorio e devono essere somministrati. Ora, immaginiamo pure che Babbo Natale possa consegnarci nel porto di Genova una nave porta-container carica di tutte queste fiale, magari proprio il 25 dicembre.

La prima domanda che mi pongo è :“Abbiamo scritto per tempo la letterina a Santa Claus?”. In altre parole, esiste un vero e proprio ordine di acquisto? Esiste una conferma da parte dei produttori? Non siamo gli unici in spasmodica attesa, esistono anche altre centinaia di paesi. Ci sarà una concorrenza spietata, peggio delle file ai negozi per i saldi. Esiste poi una pianificazione già stabilita della produzione e della consegna?  Infine, cosa succederà una volta che saranno arrivati? Siamo pronti con l’organizzazione per gestirli? La recente esperienza con il vaccino antiinfluenzale  mi crea qualche preoccupazione.

Pensiamo poi a quel vaccino che  deve essere conservato a 70 gradi sotto zero. Non è possibile tenerlo nel freezer di casa e trasportarlo in una comune borsa termica, ma ci vogliono magazzini, veicoli, centri di distribuzione e dispensari (medici di base?) tutti attrezzati per mantenere la catena del freddo a quella bassissima temperatura. Ho cercato su Google che tipo di congelatori esistono e ne ho trovati alcuni prodotti anche in Italia. Il loro prezzo parte dai 10.000 euro. In Italia abbiamo circa 34.000 medici di base. Se ognuno necessitasse di un tale super-frigo, la spesa sarebbe 340 milioni di euro. Non poco, ma affrontabile. Il vero problema sta nel tempo necessario per produrli e consegnarli, come è avvenuto per i famosi banchi a rotelle per le scuole.

Risposta al Quiz: tutti e tre i grafici rappresentano esattamente gli stessi dati. Ciò che cambia è la scala dell’asse verticale (ordinate), in A parte da 90, in B da zero e in C  è logaritmica. Però l’impressione è che B mostri una crescita molto più veloce e C una crescita del tutto trascurabile.